The difficulties of executing simple algorithms: Why brains make mistakes computers don't.

Every age has its metaphors. The brain has been compared to pneumatic machines and vacuum tubes and switchboards, and so it wasn’t surprising that with the birth of digital computing in the mid-20^th century, the dominant metaphor of the brain has been the computer. It’s not entirely an overstatement that “The brain is a computer” metaphor gave birth to the field of cognitive science, which rose out of the ashes of behaviorism. Behaviorists focused on observable behavior and didn’t much care about the computations that made it possible. The young field of cognitive science focused instead on information processing. The brain, it was argued, was best understood by the computations it performs. This made it possible to have a science that could separate itself from the hardware (neurons and all that wet stuff) and focus instead on the software (the computations). So, just as it’s possible to program (and understand principles of programming) without needing to worry about the hardware, so it was thought the same could be done for understanding the brain as an information processing device.

Computers (the modern digital kind) break apart problems into into simple arithmetic/logical operations. Any problem that is computatble (which is pretty much everything) is broken down into simple arithmetic/logical operations. Every computation a computer performs is therefore based on simple rules. This seduced cognitive scientists into thinking that biological brains worked similarly with neuron assemblies essentially implementing circuit boards that executed logical operations, and by doing clever experiments that map out the input-output relationships one could figure out what program the brain was running. Over the decades, cognitive scientists have attempted to come up with computational models of all sorts of behaviors from perception, to reasoning, to language, to memory, that are their core, rooted in the metaphor that the mind is not just a computer, it’s a digital sort of computer that implements highly complex behaviors (like language) in terms of simple arithmetic/logical rules.

If all the complicated things that people do are implemented by breaking the problems into simple formal operations, one might expect that it is trivial to perform on tasks that simply ask people to do the simple logical operations directly. It comes as a surprise then, that people turn out to be quite bad at following even the simplest rules.

The incident that inspired the paper I describe below was a Slate Magazine story from last year in which Rick Hasen, a law professor specializing in voting rights, wrote about a junior judge election in Hamilton County, OH. There was an ongoing legal action because a bunch of people’s votes were disqualified on various technicalities. One of these involved poll workers who were supposed to send people to different polling stations depending on whether their addresses were odd or even. A poll worker testified that he sent a voter with the address “798” to vote in the precinct for voters with odd-numbered addresses because he believed that 798 was an odd number.

This paper attempts, through a series of very simple tasks, to show that people’s performance is inconsistent with following very simple rules (which they can articulate just fine).

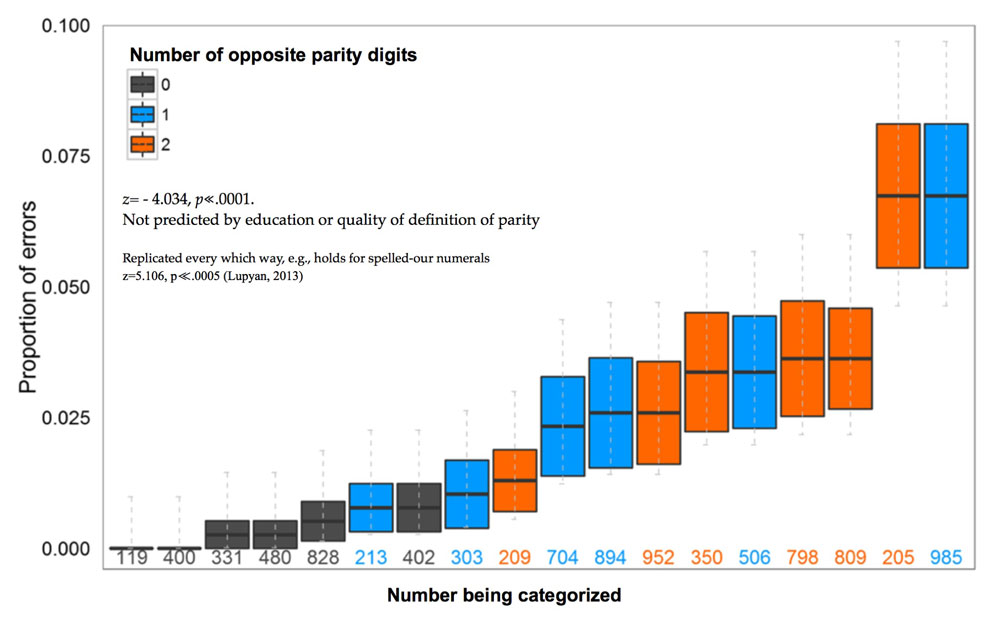
Let’s return to the number 798. The error made by the poll-worker could be a fluke. Or, it could be a consequence of this person just not knowing the rule for distinguishing odd numbers from even numbers. But it could also hint at something deeper: that such errors are actually endemic of human cognition. Even someone who knows full well how to compute whether a number is odd or even and someone who knows that all integers are either even or odd, may nevertheless represent 798 as a number that is almost odd and hence be likely to make more mistakes than on more typically even numbers like 400.

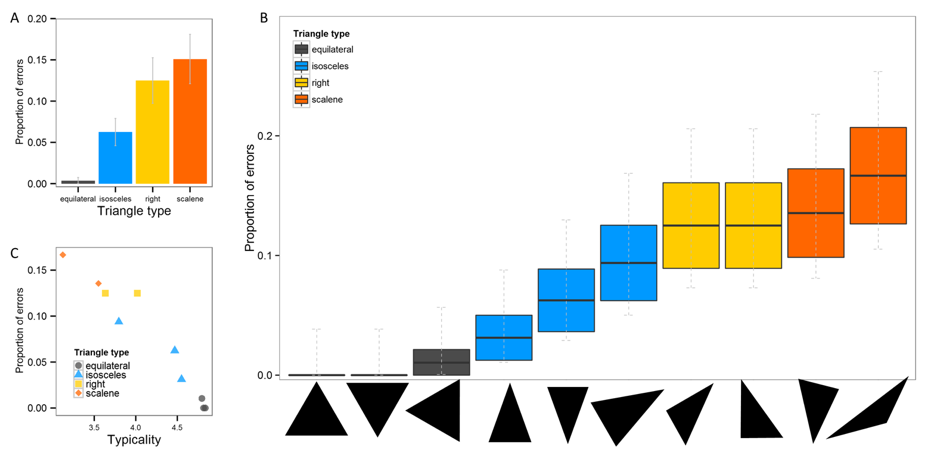
Participants(about 1200 across 13 experiments tested both in the lab and online) were given a variety of simple tasks which required that participants to place items (e.g., numbers, shapes) into formally defined categories like odd/even or triangle. These categories are “formal” because there are strict necessary and sufficient conditions for membership: a number is even if and only if it is divisible by 2 without a remainder, or  a shape is a triangle if and only if it is a three-sided planar figure. It turns out that regardless of people’s education or knowledge of parity, people made errors. About 30% of the participants we tested made at least one error on judging numerical parity, for instance, and virtually all those errors were on numbers like 798. We rule out simple attentional problems (such as accidentally focusing on the first digit instead of last digit). Similar results were obtained for classifying shapes. People can tell you what a triangle is, but everyone thinks that an equilateral triangle is a “better” triangle than a scalene one. More importantly, when simply asked to “click on all the triangles” people systematically neglected the atypical shapes. A sizeable minority fail to select scalene triangles as triangles. When explicitly told that all numbers have angles that add up to 180^o and then asked to choose the shapes with angles adding up to 180^o a sizeable minority again failed to select the atypical triangles, justifying their answers with statements like “it didn’t look like its angles added up to 180^o).

These patterns of results show that following simple rules, even for people with considerable experiments with formal systems (judging by their education), is more difficult than one would expect from the account that brains implement formal logical operations. For example, scientists have proposed that complex behaviors like language comprehension can be described in terms of following sets of complex rules. But if processing language relies on following complex rules, how do we reconcile people’s effortlessness in processing language, recognizing faces, etc., with relative difficulty to follow simple formal rules given to them? I argue in the paper that the way to reconcile this apparent paradox is that complex human behaviors like language comprehension actually do not involve following rules. We are—to various degrees—effective at approximating rules, but never fully abstract from the details of the input. This preserved input-sensitivity is critical for obtaining the enormous behavioral flexibility that humans have. To take a trivial case: consider that we can understand phrases such as “click on the upside-down triangle” which should be impossible to make sense of if we represented triangles in a symbolic way that abstracted from their (canonically horizontal) orientation. Such abstraction failures, however, may come at the cost to the ability to perform certain kinds of formal computations. But that is, after all, what we invented computers for!

So what to make of all this? If human algorithms cannot be trusted to produce unfuzzy representations of odd numbers, triangles, and grandmothers (yep, grandmothers—see the paper), the idea that they can be trusted to do the heavy lifting of moment-to-moment cognition—inherent in the metaphor of mind as digital computer—needs to be seriously reconsidered.

Rather than performing logical/arithmetic operations on the input like digital-computer algorithms human algorithms may specialize in representing inputs in terms of conditional probability distributions. This makes possible the sort of flexibility and context dependence that humans (and many non-human animals) are good at, and computers are terrible at. In contrast, it makes it hard to figure out reliably whether a number is odd or even. Although following simple rules is surprisingly difficult, some people are better at it than others, and as a society we have invented devices that are capable of blindingly fast and perfectly accurate formal computations, which on some level requires us to think in a very formal way. So the question we are left with is not why people sometimes mistake 798 for an odd number, but how people ever transcend these limitations, which appear to be inherent to how brains compute.

Copyright: © 2013 Gary Lupyan. The above content is licensed under the Creative Commons Attribution License (CC-BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.